Understanding Recursion

One of the most interesting concepts in intermediate programming is recursion. I used the word intermediate because you usually do not need it for simple tasks.

What is Recursion

In simple words, recursion is a process whereby a program function calls itself. Take for example, you make a call to your phone with your phone ( except that it doesn't ring ).

Okay, that doesn't sound so simple so here's a simple code block:

A recursive function

So what does the function above do?

The second line where we self-invoked the function, repeats whatever the original does. However, the function above is erroneous and will return an error if I try to mimic it. I'll explain better later in the article, let's have a look at the complexity of a recursive function.

Complexity of a recursive function

The time complexity for a recursive function is O(b^d) where b is the branching factor and d is the depth of the recursion.

Branching factor in recursion is determined by the formula used for executing the recursive calls. For a Fibonacci function, the branching factor is 2 since the recursive formula is Fib(n-1) + Fib(n-2).

So, I can conclude that the branching factor b is equal to length of the recursive function invoked in one call:

b => recursiveCall(x) + ... + n where n >= 0

The depth of a recursion tree is the longest path of the recursive tree. Most times, the depth of a recursive function is equal to the argument or length of argument passed into the parent function.

d => length of tree - 1

What is a recursion tree?

A recursion tree is basically a normal tree. It is only used to illustrate the recursive process such as branching and finding the depth of the recursion.

It is particularly useful to understand the execution process of a recursive function.

Defining a recursive function

A recursive function is just another normal function except that it calls itself. The fact that it calls itself requires that we set break clauses in the parent function. Like I said earlier, mimicking the earlier function will lead into an error. This error is the Maximum recursion depth exceeded error. Let's take a look at an example:

def sayHello(name):
    print("Hello ", name)
    return sayHello(name)

sayHello("a")

Running the code above will keep printing Hello Abdul until the maximum memory allocated for that function is finished:

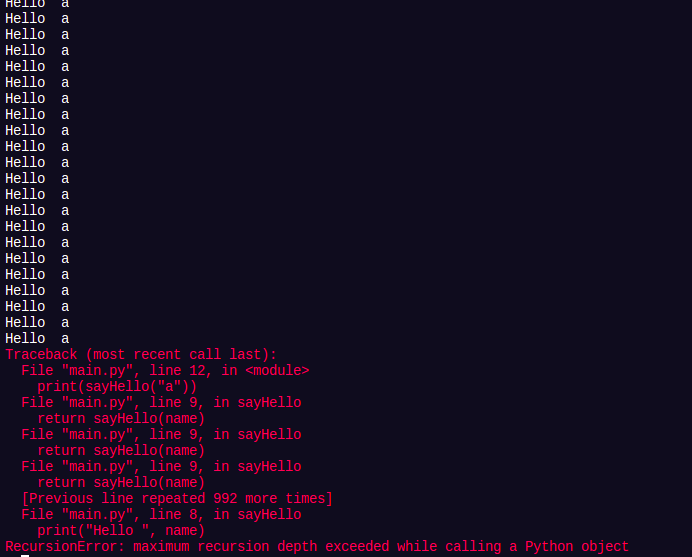
Maximum recursion stack depth exceeded

In simple words, it's like an infinite loop except that it'll crash when the limit has exceeded.

Another example is:

def recursiveSum(n):
  return n + recursiveSum(n-1)

The summation function above executes to death because we keep repeating, repeating, repeating until we've used the maximum allocations.

How do I fix that?

Like I said earlier, recursive functions need break clauses. For the summation function above, we intend to find the sum of n numbers i.e if n => 5, it should return 1 + 2 + 3 + 4 + 5 = 15.

The subsequent call to the recursive function above takes in an argument of n-1. That is, the general idea behind the function is:

if n => 5

then:

recusriveSum(5) => 5 + recursiveSum(4)
recursiveSum(4) => 9 + recursiveSum(3) 
recursiveSum(3) => 3 + recursiveSum(2) 
recursiveSum(2) => 2 + recursiveSum(1) 
recursiveSum(1) => 1 + recursiveSum(0)
recursiveSum(0) => 0 
... loops on

From the demonstration above, it is evident we need to end the function and return the answer when n-1 becomes 0. So, before invoking the recursive function, we'll set a break clause:

def recursiveSum(n):
  if n <= 1:    return n  
  return n + recursiveSum(n-1)

The break clauses immediately returns the sum once n - 1 => 0.

The recursion tree for the function above is:

From the recursion tree, the branching factor is 1 and, the depth is 5.

Head and Tail recursion

There are two types of recursion. The recursiveSum(n) function above is an example of tail recursion.

In a head recursion, the recursive function is placed at the top of the function before executing the other part of the function.

Example:

def headrecur(x):
    headrecur(x)
    do_something()

In a tail recursion, the recursive function is invoked at the end of the program:

def tailrecur(x):
    do_something()
    tailrecur(x)

In most cases, the type of recursion depends on what you intend to achieve. The tail recursion is much more popular as most recursive functions require break clauses and a result, the recursion call comes after the conditions.

You should read this Stack Overflow Answer if you do not understand.

Recursion vs Iteration

Some recursive problems can be solved iteratively. In most cases, the iterative solutions to problems are much more efficient than the recursive ones - this is because the memory consumption from iterative processes is less than that of a recursive process.

Both style have their questions, it's usually better to solve tree related problems with the recursive approach, it saves stress and time. Recursion can however be very slow in some cases - backtracking for example.

Conclusion

In this little post, I touched down the fundamentals of recursion and, the recursion tree. In future posts, I'll be solving recursion based problems alongside explaining other aspects - recursion stack, call stack generally.